MATEMÁTICA II
Considere o gráfico de y = f(x) abaixo:
%2Cnull%2C0%2C0%2C%2C%2Cblack%2C1%2Cnone)
Em que x são os valores da abscissa, e y os valares da ordenada.
O gráfico de y = f(x) pode ser representado pela função f(x) igual a:
%7D%7D%7D%3D%7B%5Cleft%7C%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D%7Bx%7D%2B%7B2%7D%5Cright%7C%7D)
%7D%7D%7D%3D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B2%7D)
%7D%7D%7D%3D%7B%5Cleft%7C%7Bx%7D%2B%7B1%7D%5Cright%7C%7D)
%7D%7D%7D%3D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7B3%7D%7Bx%7D%2B%7B2%7D)
%7D%7D%7D%3D%7B%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D%2B%7B2%7D)
A soma das raízes da equação %7D%5Cright%7C%7D%3D%7B1%7D) é exatamente:
é exatamente:
- 1
- 1/2
2
1
1/2
Sejam f e g funções reais, sendo que f(x) = 2x – 4 e g(x) = 6x – 10. Então g(f(3)) é exatamente:
4
2
1
0
3
Dados %7D%7D%7D%3D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7B2%7D%7Bx%7D%2B%7B4%7D) e
e %7D%7D%7D%3D%7Bx%7D-%7B3%7D) . O valor de x que satisfaz a condição
. O valor de x que satisfaz a condição %7D%7D%7D%5Cright)%7D%7D%7D%3D%7Bg%7B%7B%5Cleft(%7Bf%7B%7B%5Cleft(%7Bx%7D%5Cright)%7D%7D%7D%5Cright)%7D%7D%7D) é exatamente:
é exatamente:
3
0
2
4
1
Considere o esboço a seguir,
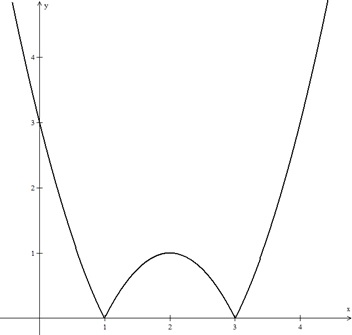
A lei de formação que representa o esboço acima é dado por:





Dadas as funções reais f(x) = 3x – 4 e g(x) = ax + b, se f[g(x)] = 6x + 5 , o valor de a - b é:
-1
-2
0
2
1
Indique o gráfico da função definida por %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B1%7D%5C%5C%7Bx%7D-%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B1%7D%7D%5Cright.%7D.)
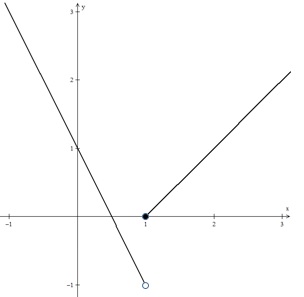
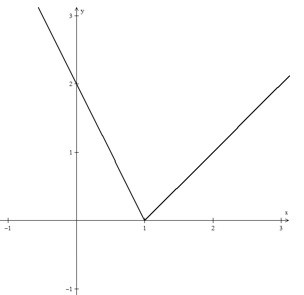
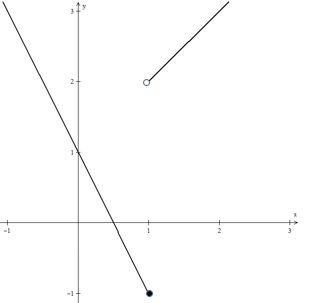
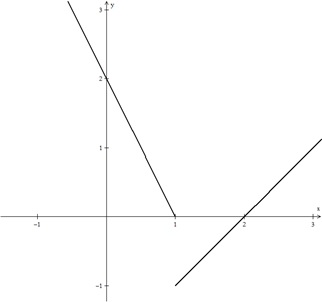
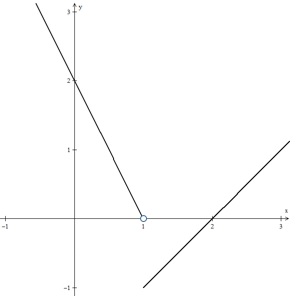
As leis seguintes representam as estimativas de valores (em milhares de reais) de dois apartamentos A e B (adquiridos na mesma data), decorridos t anos da data da compra:
Apartamento A: V = 2t + 1 + 120 Apartamento B: V = 6.2t - 2 + 248
O tempo necessário a partir da data de aquisição para que ambos tenham valores iguais é igual a:
10
4
12
8
6
Um aplicador deposita R$ 100 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,59% sobre o saldo, estabelecendo a relação %7D%3D%7B100000%7D%7B%7B%5Cleft(%7B1%7D%2C%7B0059%7D%5Cright)%7D%7D%5E%7B%7BT%7D%7D) que expressa o saldo S em função do tempo t em meses.
que expressa o saldo S em função do tempo t em meses.
O tempo necessário para que o rendimento seja igual R$ 11169, 73 é aproximadamente:
A soma das raízes da equação %7D%5Cright%7C%7D%3D%7B1%7D) é exatamente:
é exatamente:
- 1
- 1/2
2
1
1/2
Sejam f e g funções reais, sendo que f(x) = 2x – 4 e g(x) = 6x – 10. Então g(f(3)) é exatamente:
4
2
1
0
3
Dados %7D%7D%7D%3D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7B2%7D%7Bx%7D%2B%7B4%7D) e
e %7D%7D%7D%3D%7Bx%7D-%7B3%7D) . O valor de x que satisfaz a condição
. O valor de x que satisfaz a condição %7D%7D%7D%5Cright)%7D%7D%7D%3D%7Bg%7B%7B%5Cleft(%7Bf%7B%7B%5Cleft(%7Bx%7D%5Cright)%7D%7D%7D%5Cright)%7D%7D%7D) é exatamente:
é exatamente:
3
0
2
4
1
Considere o esboço a seguir,

A lei de formação que representa o esboço acima é dado por:





Dadas as funções reais f(x) = 3x – 4 e g(x) = ax + b, se f[g(x)] = 6x + 5 , o valor de a - b é:
-1
-2
0
2
1
Indique o gráfico da função definida por %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B1%7D%5C%5C%7Bx%7D-%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B1%7D%7D%5Cright.%7D.)





As leis seguintes representam as estimativas de valores (em milhares de reais) de dois apartamentos A e B (adquiridos na mesma data), decorridos t anos da data da compra:
Apartamento A: V = 2t + 1 + 120 Apartamento B: V = 6.2t - 2 + 248
O tempo necessário a partir da data de aquisição para que ambos tenham valores iguais é igual a:
10
4
12
8
6
Um aplicador deposita R$ 100 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,59% sobre o saldo, estabelecendo a relação %7D%3D%7B100000%7D%7B%7B%5Cleft(%7B1%7D%2C%7B0059%7D%5Cright)%7D%7D%5E%7B%7BT%7D%7D) que expressa o saldo S em função do tempo t em meses.
que expressa o saldo S em função do tempo t em meses.
O tempo necessário para que o rendimento seja igual R$ 11169, 73 é aproximadamente:
- 1
- 1/2
2
1
1/2
Sejam f e g funções reais, sendo que f(x) = 2x – 4 e g(x) = 6x – 10. Então g(f(3)) é exatamente:
4
2
1
0
3
Dados %7D%7D%7D%3D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7B2%7D%7Bx%7D%2B%7B4%7D) e
e %7D%7D%7D%3D%7Bx%7D-%7B3%7D) . O valor de x que satisfaz a condição
. O valor de x que satisfaz a condição %7D%7D%7D%5Cright)%7D%7D%7D%3D%7Bg%7B%7B%5Cleft(%7Bf%7B%7B%5Cleft(%7Bx%7D%5Cright)%7D%7D%7D%5Cright)%7D%7D%7D) é exatamente:
é exatamente:
3
0
2
4
1
Considere o esboço a seguir,

A lei de formação que representa o esboço acima é dado por:





Dadas as funções reais f(x) = 3x – 4 e g(x) = ax + b, se f[g(x)] = 6x + 5 , o valor de a - b é:
-1
-2
0
2
1
Indique o gráfico da função definida por %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B1%7D%5C%5C%7Bx%7D-%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B1%7D%7D%5Cright.%7D.)





As leis seguintes representam as estimativas de valores (em milhares de reais) de dois apartamentos A e B (adquiridos na mesma data), decorridos t anos da data da compra:
Apartamento A: V = 2t + 1 + 120 Apartamento B: V = 6.2t - 2 + 248
O tempo necessário a partir da data de aquisição para que ambos tenham valores iguais é igual a:
10
4
12
8
6
Um aplicador deposita R$ 100 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,59% sobre o saldo, estabelecendo a relação %7D%3D%7B100000%7D%7B%7B%5Cleft(%7B1%7D%2C%7B0059%7D%5Cright)%7D%7D%5E%7B%7BT%7D%7D) que expressa o saldo S em função do tempo t em meses.
que expressa o saldo S em função do tempo t em meses.
O tempo necessário para que o rendimento seja igual R$ 11169, 73 é aproximadamente:
4
2
1
0
3
Dados %7D%7D%7D%3D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7B2%7D%7Bx%7D%2B%7B4%7D) e
e %7D%7D%7D%3D%7Bx%7D-%7B3%7D) . O valor de x que satisfaz a condição
. O valor de x que satisfaz a condição %7D%7D%7D%5Cright)%7D%7D%7D%3D%7Bg%7B%7B%5Cleft(%7Bf%7B%7B%5Cleft(%7Bx%7D%5Cright)%7D%7D%7D%5Cright)%7D%7D%7D) é exatamente:
é exatamente:
3
0
2
4
1
Considere o esboço a seguir,

A lei de formação que representa o esboço acima é dado por:





Dadas as funções reais f(x) = 3x – 4 e g(x) = ax + b, se f[g(x)] = 6x + 5 , o valor de a - b é:
-1
-2
0
2
1
Indique o gráfico da função definida por %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B1%7D%5C%5C%7Bx%7D-%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B1%7D%7D%5Cright.%7D.)





As leis seguintes representam as estimativas de valores (em milhares de reais) de dois apartamentos A e B (adquiridos na mesma data), decorridos t anos da data da compra:
Apartamento A: V = 2t + 1 + 120 Apartamento B: V = 6.2t - 2 + 248
O tempo necessário a partir da data de aquisição para que ambos tenham valores iguais é igual a:
10
4
12
8
6
Um aplicador deposita R$ 100 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,59% sobre o saldo, estabelecendo a relação %7D%3D%7B100000%7D%7B%7B%5Cleft(%7B1%7D%2C%7B0059%7D%5Cright)%7D%7D%5E%7B%7BT%7D%7D) que expressa o saldo S em função do tempo t em meses.
que expressa o saldo S em função do tempo t em meses.
O tempo necessário para que o rendimento seja igual R$ 11169, 73 é aproximadamente:
3
0
2
4
1
Considere o esboço a seguir,

A lei de formação que representa o esboço acima é dado por:





Dadas as funções reais f(x) = 3x – 4 e g(x) = ax + b, se f[g(x)] = 6x + 5 , o valor de a - b é:
-1
-2
0
2
1
Indique o gráfico da função definida por %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B1%7D%5C%5C%7Bx%7D-%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B1%7D%7D%5Cright.%7D.)





As leis seguintes representam as estimativas de valores (em milhares de reais) de dois apartamentos A e B (adquiridos na mesma data), decorridos t anos da data da compra:
Apartamento A: V = 2t + 1 + 120 Apartamento B: V = 6.2t - 2 + 248
O tempo necessário a partir da data de aquisição para que ambos tenham valores iguais é igual a:
10
4
12
8
6
Um aplicador deposita R$ 100 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,59% sobre o saldo, estabelecendo a relação %7D%3D%7B100000%7D%7B%7B%5Cleft(%7B1%7D%2C%7B0059%7D%5Cright)%7D%7D%5E%7B%7BT%7D%7D) que expressa o saldo S em função do tempo t em meses.
que expressa o saldo S em função do tempo t em meses.
O tempo necessário para que o rendimento seja igual R$ 11169, 73 é aproximadamente:

Dadas as funções reais f(x) = 3x – 4 e g(x) = ax + b, se f[g(x)] = 6x + 5 , o valor de a - b é:
-1
-2
0
2
1
Indique o gráfico da função definida por %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B1%7D%5C%5C%7Bx%7D-%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B1%7D%7D%5Cright.%7D.)





As leis seguintes representam as estimativas de valores (em milhares de reais) de dois apartamentos A e B (adquiridos na mesma data), decorridos t anos da data da compra:
Apartamento A: V = 2t + 1 + 120 Apartamento B: V = 6.2t - 2 + 248
O tempo necessário a partir da data de aquisição para que ambos tenham valores iguais é igual a:
10
4
12
8
6
Um aplicador deposita R$ 100 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,59% sobre o saldo, estabelecendo a relação %7D%3D%7B100000%7D%7B%7B%5Cleft(%7B1%7D%2C%7B0059%7D%5Cright)%7D%7D%5E%7B%7BT%7D%7D) que expressa o saldo S em função do tempo t em meses.
que expressa o saldo S em função do tempo t em meses.
O tempo necessário para que o rendimento seja igual R$ 11169, 73 é aproximadamente:
-1
-2
0
2
1
Indique o gráfico da função definida por %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B1%7D%5C%5C%7Bx%7D-%7B1%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B1%7D%7D%5Cright.%7D.)





As leis seguintes representam as estimativas de valores (em milhares de reais) de dois apartamentos A e B (adquiridos na mesma data), decorridos t anos da data da compra:
Apartamento A: V = 2t + 1 + 120 Apartamento B: V = 6.2t - 2 + 248
O tempo necessário a partir da data de aquisição para que ambos tenham valores iguais é igual a:
10
4
12
8
6
Um aplicador deposita R$ 100 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,59% sobre o saldo, estabelecendo a relação %7D%3D%7B100000%7D%7B%7B%5Cleft(%7B1%7D%2C%7B0059%7D%5Cright)%7D%7D%5E%7B%7BT%7D%7D) que expressa o saldo S em função do tempo t em meses.
que expressa o saldo S em função do tempo t em meses.
O tempo necessário para que o rendimento seja igual R$ 11169, 73 é aproximadamente:





As leis seguintes representam as estimativas de valores (em milhares de reais) de dois apartamentos A e B (adquiridos na mesma data), decorridos t anos da data da compra:
Apartamento A: V = 2t + 1 + 120 Apartamento B: V = 6.2t - 2 + 248
O tempo necessário a partir da data de aquisição para que ambos tenham valores iguais é igual a:
10
4
12
8
6
Um aplicador deposita R$ 100 000, 00 numa caderneta de poupança. Mensalmente são creditados 0,59% sobre o saldo, estabelecendo a relação %7D%3D%7B100000%7D%7B%7B%5Cleft(%7B1%7D%2C%7B0059%7D%5Cright)%7D%7D%5E%7B%7BT%7D%7D) que expressa o saldo S em função do tempo t em meses.
que expressa o saldo S em função do tempo t em meses.
O tempo necessário para que o rendimento seja igual R$ 11169, 73 é aproximadamente:
10
4
12
8
6